28 KiB
人工智能实验盲目搜索
一、 无信息搜索(盲目搜索)
1. 算法原理
1.1 搜索问题的形式化定义
解决搜索问题时,首先需要对搜索问题进行形式化表述。搜索问题从以下几个方面表述:
- 状态空间:对问题的形式化,表示需要进行搜索的空间
- 动作:对真正动作的形式化,表示从一个状态到达另一个状态
- 初始状态:表示当前的状态
- 目标:表示需要达到的目标的状态
- 启发方法:用于指挥搜索的前进方向的方法
- 问题的解:一个从初始状态到达目标状态的动作序列
搜索问题可以用状态空间树表示,每个节点对应着状态空间中的一种状态。节点的父节点表示产生该状态的上一个状态,父节点生成子节点时需要记录生成节点所采取的行动与代价。
搜索算法的性能需要考虑一个方面:
- 完备性:当问题有解时是否一定能找到解
- 最优性:搜索策略是否一定能找到最优解
- 时间复杂度:找到解所需要的时间,又称为搜索代价
- 空间复杂度:执行搜索过程中需要多少内存空间
1.2 无信息搜索的具体算法
1.2.1 宽度优先搜索
宽度优先搜索用一个先进先出的队列实现,节点的拓展顺序与目标节点的位置无关。从状态空间树上看,宽度优先搜索的拓展顺序是按树的层次顺序来进行的。这样一来,短的路径会在任何比它长的路径之前被遍历,因此宽度优先搜索具有完备性和最优性。
定义b为问题中一个状态最大的后继状态个数,d为最短解的动作个数,则有:
- 时间复杂度:
1+b+b^2+...+b^d+b(b^d-1)=O(b^{d+1}) - 空间复杂度:
b(b^d-1)=O(b^{d+1})
1.2.2 深度优先搜索
把当前要扩展的状态的后继状态放在边界的最前面,边界上总是扩展最深的那个节点。在状态空间无限或在状态空间有限,但是存在无限的路径(例如存在回路) 的情况下不具有完备性。在状态空间有限,且对重复路径进行剪枝的情况下才有。不具有最优性。
定义m是遍历过程中最长路径的长度,则有:
-
时间复杂度:
O(b^m) -
空间复杂度:
O(bm)
1.2.3 一致代价搜索
边界中,按路径的成本升序排列,总是扩展成本最低的那条路径。当每种动作的成本是一样的时候,和宽度优先是一样的。假设每个动作的成本都大于某个大于0的常量,所有成本较低的路径都会在成本高的路径之前被扩展。给定成本,该成本的路径数量是有限的;成本小于最优路径的路径数量是有限的,最终,我们可以找到最短的路径,因此具备完备性和最优性。
对于一致代价搜索,当最优解的成本为C* ,上述最低代价为 s,则有:
- 时间复杂度:
O(b^{[C^*/s]+1}) - 空间复杂度:
O(b^{[C^*/s]+1})
1.2.4 深度受限搜索
深度受限搜索是深度优先搜索,但是预先限制了搜索的深度L,因此无限长度的路径不会导致深度优先搜索无法停止的问题。 但只有当解路径的长度 ≤ L 时,才能找到解,故不具有完备性和最优性。
- 时间复杂度:
O(b^L) - 空间复杂度:
O(bL)
1.2.5 迭代加深搜索
一开始设置深度限制为L = 0,迭代地增加深度限制,对于每个深度限制都进行深度受限搜索 。如果找到解,或者深度受限搜索没有节点可以扩展的时候可以停止当前迭代,并提高深度限制L 。如果没有节点可以被剪掉(深度限制不能再提高)仍然 没有找到解,那么说明已经搜索所有路径,因此这个搜索不存在解。具有完备性,且在每个动作的成本一致时具有最优性。
- 时间复杂度:
(d+1)b^0+db+(d-1)b^2+...+b^d=O(b^d) - 空间复杂度:
O(bd)
1.2.6 双向搜索
同时进行从初始状态向前的搜索和从目标节点向后搜索,在两个搜索在中间相遇时停止搜索。假设两个搜索都使用宽度优先搜索,则具有完备性,在每条边/每个动作的成本一致的情况下具有最优性。
- 时间复杂度:
O(b^{d/2}) - 空间复杂度:
O(b^{d/2})
2. 流程图和伪代码
为了便于比较算法差异,我实现了宽度优先搜索和双向搜索两种算法。
2.1 宽度优先搜索
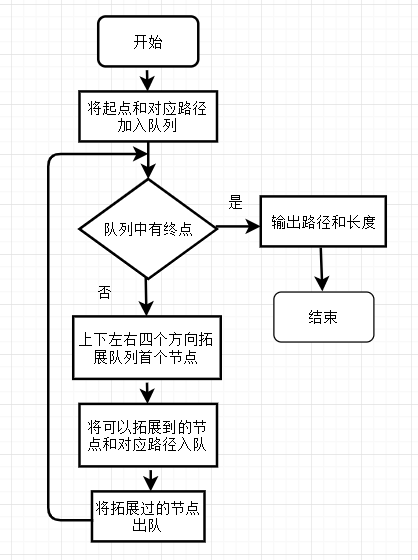
判断队列是否有终点和输出路径较为简单,下面只讨论算法终点部分。
每次取出队列首个节点,记其坐标为(x,y),向上下左右四个方向拓展新的四个节点。拓展节点的方式如下:
input: queue
/* 输入当前节点队列 */
output: queue
/* 输出更新后的队列 */
def expand(queue)
(x,y) = queue.front(); /* 取出队首的节点 */
/* 向上下左右四个方向拓展新的节点 */
expand_node(x+1,y);
expand_node(x-1,y);
expand_node(x,y+1);
expand_node(x,y-1);
/* 将当前节点出队 */
queue.pop();
判断具体的节点是否要加入队列时,判断节点位置是否是通路'0'或终点'E'即可。考虑到迷宫四周一圈都是墙壁'1',所以不需要考虑出界的问题。
input: queue, x, y
/* 输入当前节点队列,要加入的新节点的坐标 */
output: queue
/* 输出更新后的队列 */
def expand_node(queue, x, y)
if (x,y) 处为通路或终点
then
queue.push((x,y))
将(x,y)处变为墙壁
2.2 双向搜索
在宽度优先搜索的基础上应用双向搜索。原先的单个队列变为由起点和终点拓展成的两个队列,当两个队列元素有交集时找到相应的路径。两个队列都为空时无解,流程图只给出了一般的求解步骤,没有加入判断无解的情况,在代码中考虑了这一问题。
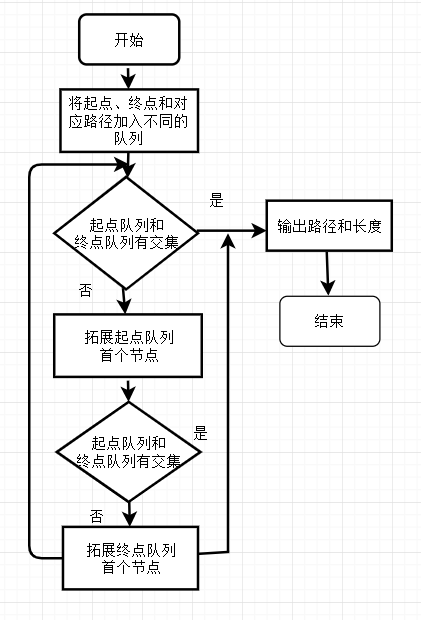
拓展节点和判断节点是否加入队列和一般的宽度优先搜索一样,不再赘述。底下的具体代码会给出具体的分析。
3. 代码展示
3.1 数据预处理和特殊变量声明
读入迷宫数据的代码如下:
maze = []
with open('MazeData.txt', 'r') as f:
for eachLine in f:
line = []
for eachPos in eachLine:
if eachPos == '\n':
break
line.append(eachPos)
maze.append(line)
将迷宫数据存储为一个二维数组,每个位置存储一个字符,表示当前迷宫位置的状态,分为四种:
'0':可通行的道路'1':不可通行的墙壁'S':起点'E':终点
在之后所有算法实现中,使用:
expanded = set()
expanded是拓展过的所有节点的集合,用于最后比较算法效果。
3.2 宽度优先搜索
首先将起点加入队列,并记录对应的路径。其中,node_list是当前所有的可扩展节点的队列,path是从起点到当前节点的路径,与node_list每个节点的下标一一对应。
初始化:
# 获取迷宫大小
row = len(maze)
col = len(maze[0])
node_list = [] # 可拓展节点队列
path = [] # 起点到可拓展节点的路径
end_node = [] # 终点的坐标
expanded = set()# 记录所有可扩展节点的集合
for i in range(row):
for j in range(col):
if maze[i][j] == 'S':
node_list.append([i,j]) # 将起点加入可扩展节点队列
path.append([[i,j]]) # 记录路径(当前只有起点到起点)
expanded.add((i,j)) # 记录已经拓展的节点
if maze[i][j] == 'E':
end_node = [i,j] # 记录终点
接下来,在无限循环while 1中实现:
获取队列首个可扩展节点的坐标:
x = node_list[0][0]
y = node_list[0][1]
接着往上下左右四个方向拓展当前节点。如果拓展的新节点为终点则找到解,退出循环(下面的代码以x+1,y的向下拓展为例):
expand(x+1,y)
if end_node in node_list:
break
拓展函数的具体实现如下:
def expand(x,y):
if maze[x][y] == '0' or maze[x][y] == 'E':
node_list.append([x,y]) # 加入队列
path.append(path[0]+[[x,y]]) # 更新路径
expanded.add((x,y)) # 记录拓展的节点
maze[x][y] = '1' # 表示当前位置已经被拓展
可扩展到的节点定义为通路'0'与终点'E',如果节点可扩展到,则加入节点队列,并更新路径(父节点的路径+当前节点=当前节点路径)。注意最后要把当前位置的值改为'1'防止之后重复拓展。
拓展完节点后,将该节点和与其相对应的路径从队列中删除。
del node_list[0]
del path[0]
3.3 双向搜索
双向搜索需要两个队列,分别记录由起点和终点拓展出的节点。另外还要记录两个队列中元素的路径:
node_from_start = [] # 起点拓展的节点队列
path_from_start = [] # 上述队列节点对应路径
node_from_end = [] # 终点拓展的节点队列
path_from_end = [] # 上述队列节点对应路径
同样,在初始化时将初始的节点加入。起点和对应的路径加入起点的队列,终点和对应的路径加入终点的队列:
for i in range(row):
for j in range(col):
if maze[i][j] == 'S':
node_from_start.append([i,j]) # 起点入队
path_from_start.append([[i, j]]) # 起点路径入队
expanded.add((i,j)) # 记录所有拓展过的节点
if maze[i][j] == 'E':
node_from_end.append([i, j]) # 终点入队
path_from_end.append([[i, j]]) # 终点路径入队
expanded.add((i, j)) # 记录所有拓展过的节点
初始化find_ans = False来记录是否找到解。
在无限循环while 1中执行以下判断:
如果没有可以拓展的节点,即两个队列都为空,则迷宫无解,退出循环:
if node_from_start == [] or node_from_end == []:
find_ans = False
break
拓展起点队列的全部节点,之后判断是否与终点队列有交集:
# 拓展从起点出发的节点
node_from_start, path_from_start =
expandNode(node_from_start, path_from_start)
# 如果从起点和终点出发的节点重复,则找到解,退出循环
for eachNode in node_from_start:
if eachNode in node_from_end:
find_ans = True
break
if find_ans:
break
同样,拓展终点队列的全部节点,之后判断是否与终点队列有交集:
# 拓展从终点出发的节点
node_from_end, path_from_end = expandNode(node_from_end, path_from_end)
# 如果从起点和终点出发的节点重复,则找到解,退出循环
for eachNode in node_from_start:
if eachNode in node_from_end:
find_ans = True
break
if find_ans:
break
拓展全部节点的函数expandNode的具体实现如下:
def expandNode(node_set, path_set):
new_node_set = []
new_path_set = []
while node_set != []:
x = node_set[0][0]
y = node_set[0][1]
# 上下左右四个方向进行拓展
if maze[x+1][y] == '0':
new_node_set.append([x+1,y])
new_path_set.append(path_set[0]+[[x+1,y]])
expanded.add((x+1,y))
if maze[x-1][y] == '0':
new_node_set.append([x-1,y])
new_path_set.append(path_set[0]+[[x-1,y]])
expanded.add((x-1,y))
if maze[x][y+1] == '0':
new_node_set.append([x,y+1])
new_path_set.append(path_set[0]+[[x,y+1]])
expanded.add((x,y+1))
if maze[x][y-1] == '0':
new_node_set.append([x,y-1])
new_path_set.append(path_set[0]+[[x,y-1]])
expanded.add((x,y-1))
maze[x][y] = '1' # 将当前节点置为墙壁
expanded.add((x,y)) # 记录所有拓展的节点
del node_set[0] # 将当前节点出队
del path_set[0]
return new_node_set[:], new_path_set[:]
在双向搜索算法中对某个队列的单次拓展本质是宽度优先搜索的一次拓展。
如果起点和终点队列有交集,则find_ans == True,进行以下处理:
# 找到相交的节点
for eachNode in node_from_start:
if eachNode in node_from_end:
cross_node = eachNode
break
# 找到该节点在两个队列中对应的位置
start_idx = node_from_start.index(cross_node)
end_idx = node_from_end.index(cross_node)
# 将两个部分的路径拼接起来
ans = path_from_start[start_idx][:-1] + path_from_end[end_idx][::-1]
有节点相交,则将该节点在起点队列和终点队列对应的路径拼接起来,得到最终解的路径ans。需要注意的是,相交的节点不要重复记录,以及从终点开始拓展的节点的路径是反的,需要翻转。
4. 实验结果及分析
4.1 算法的完备性与最优性
程序最后,输出节点的拓展节点个数、路径长度(路径上的节点个数)、路径的具体步骤:
print(len(expanded))
print(len(ans))
print(ans)
宽度优先搜索和双向搜索算法的输出分别为:
从输出的路径上看,二者找到了相同的解。考虑到从状态空间树上看,宽度优先搜索的拓展顺序是按树的层次顺序来进行的。这样一来,短的路径会在任何比它长的路径之前被遍历,因此如果找到了解,绝对是开销最小的,也就是最优解。而如果存在解且解的开销优先时,小于解开销的所有路径是有限的,因此宽度优先搜索在有解时能找到解。综上,宽度优先搜索具有完备性和最优性。而我的双向搜索中,起点和终点的搜索方法都为宽度优先搜索,同样也具有完备性和最优性。
4.2 时间复杂度
定义b为问题中一个状态最大的后继状态个数,d为最短解的动作个数。理论上,宽度优先搜索的复杂度为:
而双向搜索的时间复杂度为:O(b^{d/2})。
两种算法的时间复杂度可以由二者拓展过的节点数量比较。拓展过的节点数越多,需要的运算就越多,也就越耗时。从上面的输出可以看出,宽度优先搜索算法中总共拓展了 270 个节点,而双向搜索算法只拓展了 194 个节点,由此可以看出双向搜索的确比单纯的宽度优先搜索要快。
4.3 空间复杂度
理论上,宽度优先搜索的空间复杂度为O(b^{d+1}),双向搜索为O(b^{d/2})。
在每次拓展节点后,输出队列状态:
print(list_node)
print('start:',node_from_start)
print('end:',node_from_end)
节点数最多的时候,宽度优先搜索可以达到 9 个:
而若不考虑交点,双向搜索最多的时候有 11 个:
若只考虑复杂度,双向搜索中的起点队列和终点队列的空间复杂度相同,只考虑一个即可,即最多为起点队列中的 9 个。但是在实际运行的过程中也的确出现了双向搜索的空间开销比宽度优先搜索大的情况。二者差别并不大,只相差两个节点。在迷宫更加复杂、规模更大的时候,空间复杂度的差距应该能更好地体现出来。
二、 启发式搜索
1. 算法原理
启发式搜索又叫有信息的搜索,它利用问题所拥有的启发信息来引导搜索,达到减少搜索范围,降低问题复杂度的目的。对于一个具体的问题,构造一个专用于该领域的启发式函数h(n), 该函数用于估计从节点n到达目标节点的成本 ,要求对于所有满足目标条件的节点n有:h(n)=0。
1.1 A*搜索
定义评价函数f(n)=g(n)+h(n),其中g(n)是从初始节点到达节点n的路径成本,h(n)是从n节点到达目标节点的成本的启发式估计值。 因此,f(n)是经过节点n从初始节点到达目标节点的路径成本的估计值。利用节点对应的f(n)来对边界上的节点进行排序。
A*搜索往往速度较快,但需要维护开启列表和关闭列表,并且需要反复查询状态,因此空间复杂度是指数级的。其具体步骤为:
- 将起点当做待处理点加入开启列表
- 搜索所有可以拓展的节点并加入开启列表,计算这些节点的
f(x) - 将起点从开启列表中移动到关闭列表
- 从开启列表中寻找
f(x)最小的节点,将相邻节点加入开启列表,并将该节点移动到关闭列表。若相邻节点已经在开启列表则更新它的g(x)值 - 若找到目标节点(找到解)或开启列表为空(无解)则退出,否则重复步骤 4 。
1.2 IDA*算法
IDA* 是迭代加深深度优先搜索算法(IDS)的扩展。因为它不需要去维护表,因此它的空间复杂度远远小于A* 。在搜索图为稀疏有向图的时候,它的性能会比A*更好。在算法迭代的每一步,IDA*都会进行深度优先搜索,在某一步所有可以拓展到的节点对应的最小启发函数值大于某个给定阈值则进行剪枝。具体步骤为:
- 给定估价函数
f(x)值的阈值,并将起点作为开始节点 - 计算当前节点所有邻居节点的估价函数,选取最小的一个。大于阈值的直接剪枝。
- 如果某个节点的估价函数大于阈值则将其作为下一次迭代的新的阈值
- 找到目标节点则返回结果
1.3 启发式函数的设计
- 可采纳性:假设每个状态转移(每条边)的成本是非负的,而且不能无穷地小,假设
h*(n)是从节点n到目标节点的最优路径成本(不连通则为无穷大)。当对于所有的节点n,满足h(n)<=h*(n)时,则称h(n)是可采纳的。也就是说,可采纳的启发式函数低估了当前节点到达目标节点的成本,使得实际成本最小的最优路径能够被选上。因此,对于任何目标节点g,有h(g)=0 - 一致性(单调性):对任意节点
n1和n2有:h(n1)\leq cost(n1\to n2)+h(n2)。满足一致性的启发式函数也一定满足可采纳性,大部分的可采纳的启发式函数也满足一致性/单调性。
可采纳性意味着最优性,最优解一定会在所有成本大于最优开销的路径之前被扩展到。因为一致性,搜索第一次扩展到某个状态,就是沿着最小成本的路径进行扩展的 ,而且在遍历节点n时,所有f值小于f(n)的节点都已经被遍历过了 。
也就是说,启发式函数的可采纳性和一致性是启发式搜索完备性和最优性的保证。
2. 流程图和伪代码
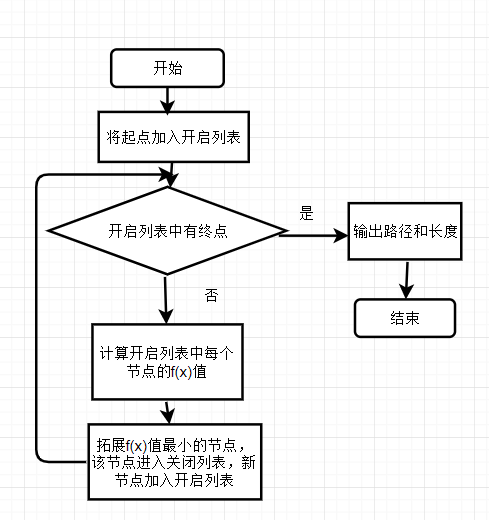
流程算法原理部分的步骤基本一致。
启发式搜索的终点在于启发式函数的设计和估价函数的计算:
input: open_list, close_list, g
/* 输入:开放列表、关闭列表、开放列表中每个元素对应的g(x)值 */
output: open_list, close_list, g
/* 输出:上述输入的更新后的结果 */
def expandNode(open_list, close_list, g)
/* 找到估价函数最小的节点 */
for each_node in openlist
f(each_node) = h(each_node) + g(each_node)
node = 有最小f(x)值的节点
/* 拓展该节点 */
expand(node)
/* 将该节点移动到关闭列表 */
close_list.append(node)
open_list.delete(node)
拓展节点的过程和上述的宽度优先搜索基本相同,这里不再赘述。之后的代码展示会详细说明细节部分。
3. 代码展示
迷宫问题中,要求找最短路径,但不能越过障碍。因此可以考虑将启发式函数设计成Lp距离,可以越过障碍。
在初始化时,考虑不再同步存储由起点到每个节点的路径而是存储每个节点的父节点(起点的父节点为None),最终通过父节点一层层回推得到路径。起点的g(x)为0。
open_list = [] # 开启列表
open_parent_node = [None] # 开启列表中每个节点对应的父节点
g = [0] # 开启列表中每个节点对应的 g(x) 值
close_list = [] # 关闭列表
close_parent_node = [] # 关闭列表中每个节点对应的父节点
在起点加入开放列表后,即可开始搜索:
find_ans = False
while 1:
# 若开启列表为空,则迷宫无解
if open_list == []:
find_ans = False
break
# 对节点进行拓展
expandNode(open_list, close_list, open_parent_node, close_parent_node, g)
# 若开放节点中存在终点节点则找到解
if end_node in open_list:
find_ans = True
break
其中在开放列表中寻找可拓展节点的具体函数如下:
def expandNode(open_list, close_list, open_parent_node, close_parent_node, g)
首先初始化参数:
min_cost = 100000 # 当前最小开销
min_idx = 0 # 开销最小的节点的下标
p = 1 # Lp距离的p
然后对开放节点中的每一个节点进行遍历,计算估计函数值。其中h(x)定义为Lp距离,g(x)由列表g给出。同时记录当前的最小估计函数值与节点,方便之后的处理:
# 找到可扩展的开销最小的节点
for i in range(len(open_list)):
h = (abs(open_list[i][0] - end_node[0])**p + abs(open_list[i][1] - end_node[1])**p ) ** (1/p)
# h = max(abs(open_list[i][0] - end_node[0]), abs(open_list[i][1] - end_node[1]))
f = h + g[i]
if f < min_cost:
min_cost = f
min_idx = i
找到后对该节点的上下左右的节点进行拓展即可:
# 将该节点的可扩展节点加入开放列表
x = open_list[min_idx][0]
y = open_list[min_idx][1]
maze[x][y] = '1' # 将当前位置变为1防止重复计算
validNode(open_list, open_parent_node, g, x, y, x+1, y, min_idx)
validNode(open_list, open_parent_node, g, x, y, x-1, y, min_idx)
validNode(open_list, open_parent_node, g, x, y, x, y+1, min_idx)
validNode(open_list, open_parent_node, g, x, y, x, y-1, min_idx)
最终将该节点加入关闭列表:
# 将该节点从开放列表中删除并加入关闭列表
close_list.append([x,y])
close_parent_node.append(open_parent_node[min_idx])
expanded.add((x,y))
del open_list[min_idx]
del open_parent_node[min_idx]
del g[min_idx]
拓展新节点的函数如下:
# 判断当前节点是否可以拓展并加入开放列表
def validNode(open_list, open_parent_node, g, x, y, x_expand, y_expand, min_idx):
if maze[x_expand][y_expand] == '0' or maze[x_expand][y_expand] == 'E':
# 若新节点已经出现在开放列表中
if [x_expand, y_expand] in open_list:
idx = open_list.index([x_expand, y_expand])
if g[idx] < g[min_idx] + 1:
g[idx] = g[min_idx] + 1
open_parent_node[idx] = [x,y]
# 若新节点不存在开放列表中
else:
open_list.append([x_expand,y_expand])
open_parent_node.append([x,y])
g.append(g[min_idx]+1)
新节点出现在开放列表中,则不需要将该节点加入开放列表,但是需要更新该节点的状态:若拓展的新节点的g(x)比记录中的小,则去小的那一个并且更新节点的父节点。否则直接将该节点加入开放列表且记录对应的父节点和开销g(x)。开销为父节点的开销 +1 。
需要注意的是,开放列表的节点是下一步可以到达的节点,而不是已经搜索过的节点,因此不需要考虑加入已拓展节点的集合。
最终将终点节点一步步向上回推父节点得到路径,逆序后即为解:
idx = open_list.index(end_node)
last_node = open_parent_node[idx]
path = [end_node]
while last_node is not None:
path.append(last_node)
last_node = close_parent_node[close_list.index(last_node)]
path = path[::-1]
4. 实验结果及分析
程序最后,输出节点的拓展节点个数、路径长度(路径上的节点个数)、路径的具体步骤:
print(len(expanded) + 1)
print(len(path))
print(path)
因为终点在开放列表中,没有算进但是应当算进已经拓展的节点,因此len(expanded)需要加 1 来修正。另外,打印的所谓的“路径长度”其实是路径上节点的个数。实际长度应该减一。
启发式函数h(x)和实际的到达终点的开销h^*(x)存在下列关系:
| 情形 | 性能 |
|---|---|
h(n)=0 |
只有g(n)起作用,退化为Dijkstra算法,保证找到最短路径 |
h(n)\leq h^*(n) |
保证找到最短路径 |
h(n)=h^*(n) |
只走最佳路线,不拓展额外节点。运行最快且保证找到最短路径 |
h(n)>h^*(n) |
不保证找到最短路径 |
我尝试不同的启发式函数的结果(包括不合理的启发式函数):
| 函数 | h(x)=0 |
Lp距离p=1 |
Lp距离p=2 |
Lp距离p=3 |
Lp距离p=\infin |
|---|---|---|---|---|---|
| 拓展节点数 | 268 | 222 | 227 | 227 | 228 |
| 路径长度 | 69 | 69 | 69 | 69 | 69 |
| 开放列表最大节点数 | 9 | 9 | 9 | 9 | 9 |
考虑到之前的宽度优先搜索拓展了270个节点,路径长度为69;双向搜索拓展了194个节点,路径长度为69,通过比较可以看出,启发式函数的加入的确相较宽度优先搜索要快(拓展的节点数少了使得计算量减少了)。而无信息搜索的双向搜索优于启发式搜索。在更大的问题规模下或者选取更好的启发式函数可能更能体现启发式搜索的优越性。
另一方面,这几种情况下开放列表最大节点数都为9,在这几种不同的启发式函数下,看不出太大的空间复杂度的区别。在更大规模的问题上可能会有更明显的差别。
下面考虑使用曼哈顿距离(L1距离)的D倍作为启发式函数。D的设计是为了距离衡量单位与启发式函数相匹配,一般取方格间移动的最小代价,在迷宫问题中就是1。为了比较效果,尝试不同的D值:
| D 值 | 0 | 0.5 | 1 | 1.5 | 2 | 3 | 4 |
|---|---|---|---|---|---|---|---|
| 拓展节点数 | 268 | 242 | 222 | 229 | 220 | 212 | 79 |
| 路径长度 | 69 | 69 | 69 | 69 | 69 | 69 | 77 |
| 开放列表最大节点数 | 9 | 8 | 9 | 8 | 8 | 8 | 6 |
D值和拓展节点数的关系如下:
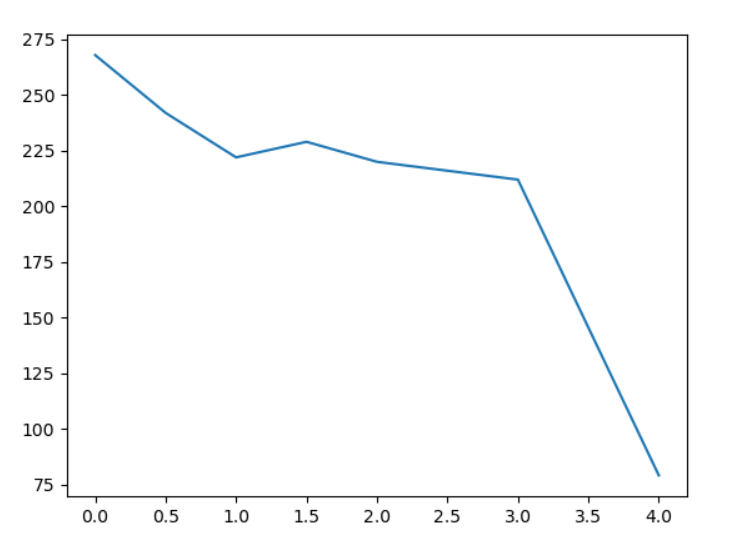
在D值较小时,拓展节点数相差不太大,其路径长度都为69可以看出,都找到了最优解。在D达到4时,可以看到拓展节点数大大下降了,从200多直接降到了79,也就是运算效率大大提升了。同时,开放列表最大节点数也有一定的下降,所占内存空间变少了。然而,在这种情况下路径长度却变成了77,也就是说找到的解不是最优解。这就对应了上述启发式函数h(n)>h^*(n)的情况,启发式函数过大找到的解不是最优的。